浅谈移动机器人定位算法的PnP问题
更新时间:2020-04-20文章来源:网络
如果已知一个3D空间点的位置p:(x,y,z),你拿着一个相机,站在某个看得到这个空间点p的地方,对着空间点p拍了一张照片。那么请问,你站在哪里拍这张照片呢?你手里拿的相机的朝向角度又是怎么样的呢?
相机就好比是移动机器人的眼睛,我们想知道移动机器人在哪里就需要求解相机现在的位置。抽象的说,现在我们已知n个3D点和n个2D点(这个3D空间点在图像中的像素位置(u,v),即在图像中的第v行,第u列),如何求2D成像点的实际位姿(位置和姿态)?对于这类问题我们统一可以抽象为一个3D-2D的PnP(Perspective-n-Point)问题。它描述了当我们知道n 个3D 空间点以及它们的投影位置时,如何估计相机所在的位姿。
对于这个问题,我们可以有多种求解方法,下面就给大家介绍几种常用、易懂的方法:
1.直接线性变换(DLT)
这种方法顾名思义,直接通过构建像素点(u,v)和空间点P:(X,Y,Z)的解析变换关系,求解出他们的解析解。使用这种方法时,我们需要6对匹配好的3D-2D的匹配点。当匹配点大于6对点时可以使用SVD(奇异值分解)等方法对超定方程求解出最小二乘解。
2.P3P
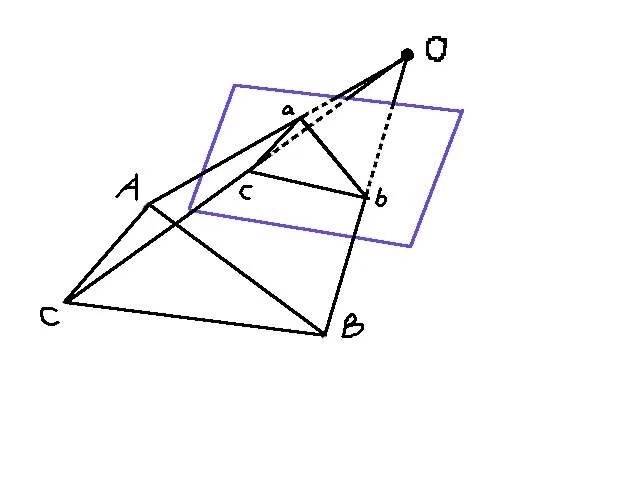
P3P至少需要3个点,利用给定的三个点的几何关系(相似关系)。如图(1)所示,记3D空间点为A,B,C。他们在相机成像平面分别为2D点:a,b,c。我们可以发现:?Oab ? ?OAB, ?Obc ? ?OBC, ?Oac ? ?OAC。求解投影点a, b, c 在相机坐标系下的3D 坐标,问题自然而然转换成一个3D 到3D 的位姿估计问题。
3.EPNP,UPNP
EPNP和UPNP是对P3P方法的改进它们利用更多的信息,主要是利用已知的3d点,通过PCA选择4个控制点,建立新的局部坐标系,从而将3d坐标用新的控制点表示出来。然后,利用相机投影模型和2d点,转换到相机坐标系中,再在相机坐标系中建立和世界坐标系同样关系(每个点在相机坐标系和世界坐标系下控制点处的坐标一致)的4个控制点,求解出相机坐标系下的四个控制点的坐标,进而利用ICP求解位姿。
4.光束平差法(Bundle Adjustment)
除了使用线性方法之外,我们可以把PnP问题构建成一个定义于李代数上的非线性最小二乘问题。这是一种近几年流行起来的非常通用的求解方式,我们可以用它对PnP 给出的结果进行优化。在PnP中,
BundleAdjustment 问题,总体来说是一个最小化重投影误差(Reprojection error)的问题。
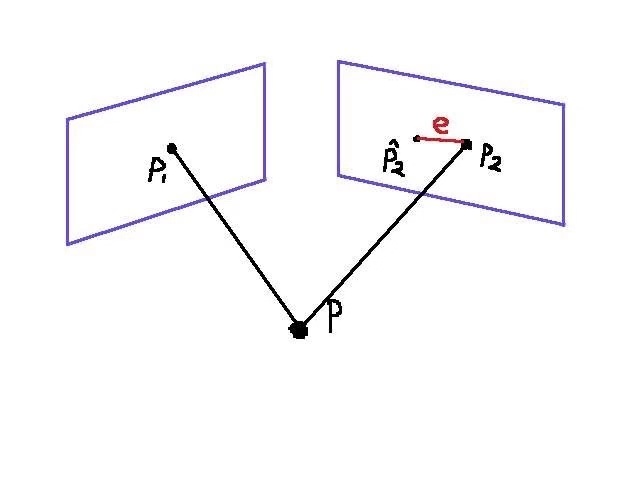
对于最小化重投影误差理解如图二所示,对于空间点P(X,Y,Z),我们按照假定的R和t去做变换,我们把P点重新投影到图像上,可以得到投影点和实际p2点之间的误差e。目标就是通过不断的迭代计算调整R和t,使得误差e尽可能的小。
以上就是一些求解方法,那我们应该怎么用呢?
Opencv给我们提供了PnP的求解器:PNPSolver,它提供了3种求解方法:CV_P3P,CV_EPNP,CV_ITERATIVE。
CV_P3P 使用了非常经典的Gao方法求解,求解出4组可能解,再通过第四个点重投影,返回重投影误差最小的点。
CV_EPNP 使用了论文EPnP:Efficient Perspective-n-Point Camera Pose Estimate的求解方法。
CV_ITERATIVE 基于Levenberg-Marquardt优化方法迭代求解,实质是迭代求出重投影误差最小的解。
